The moment of inertia is one of the most important features of the structural element, which largely determines the section selections of the engineer. It is also known as the second moment of the field.

The word inertia has meanings such as inertia, stagnation. The moment of inertia of an object corresponds to the geometric design of the engineering element as its resistance to stresses such as torsion and bending. In fact, when the moment of inertia is mentioned, most people think of the following picture. Comparison of the resistance of a beam against the same load applied to its design in two different positions.

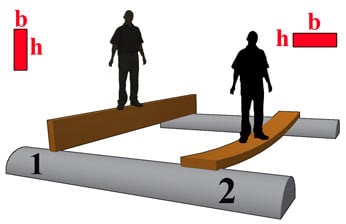
As the diagram shows, some shapes are better than others at resisting bending. Obviously, the orientation of the shape also affects bending. In a way, it roughly shows why the long part of the beam should be placed vertically.

Columns, beams and most other structural members have cross-sections similar to I, H, and C shapes. This situation brings with it some question marks:

Why aren't these elements manufactured from fully-filled simple geometries (square, circle, etc.)?
On what basis is the geometry to be chosen in the design of a structural element decided?
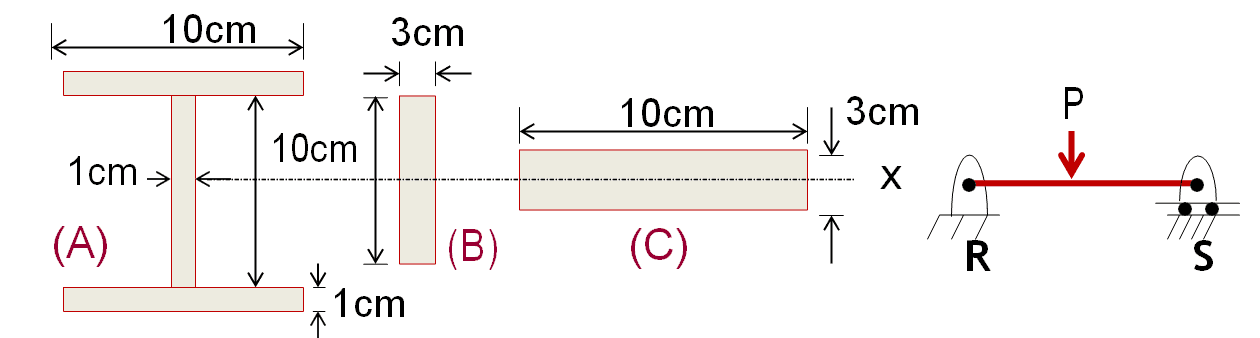
In order to find answers to these questions, it will be useful to explain the event numerically. So let's examine the following three different sections:

Let's consider three different cross-sections as above for the RS beam, A, B and C. If we consider that they are all made of the same material and calculate, the total cross-sectional areas are equal. The masses of the objects per unit length are also equal.
For the vertical P force applied beam shown on the right, which cross-section shape will result in less internal stress and deflection (collapse)?
The answer is related to the Moment of Inertia of the beam around the x-axis. Section A has the greatest inertia since most of the areas are further away from the x-axis. Therefore, less stress and deflection occur.
Although the moment of inertia, also known as the second moment of the area, varies according to the section properties, when we consider engineering structural elements, it is b.h3/12 for rectangular sections and you can watch the parallel axis theorem, which is one of the proof and calculation methods. You can inspect it from this address.

3502 Reads